Inhalt

• Schritte
• Tipps

Mathematiker und Grafikprogrammierer müssen häufig den Winkel zwischen zwei Vektoren ermitteln. Glücklicherweise erfordert die Formel zur Berechnung dieses Winkels nichts weiter als ein einfaches Skalarprodukt. Obwohl die Gründe für diese Formel bei Verwendung zweidimensionaler Vektoren leichter zu verstehen sind, können wir sie leicht an Vektoren mit einer beliebigen Anzahl von Komponenten anpassen.

Schritte

Teil 1 von 2: Berechnen Sie den Winkel zwischen zwei Vektoren

1. 

   Identifizieren Sie die beiden Vektoren. Notieren Sie alle bekannten Informationen zu den beiden Vektoren. In diesem Tutorial wird davon ausgegangen, dass Sie die Vektoren nur anhand ihrer Dimensionskoordinaten kennen (auch genannt) Komponenten). Wenn Sie das schon kennen Modul oder Standard Von diesen Vektoren (dh ihrer Länge) können Sie einige der folgenden Schritte überspringen.
   • Beispiel: Wir betrachten die zweidimensionalen Vektoren = (2,2) und = (0,3). Diese beiden Vektoren können als = 2 umgeschrieben werdenich + 2j e = 0ich + 3j = 3j.
   • Obwohl in unserem Beispiel zwei zweidimensionale Vektoren verwendet werden, können wir die folgenden Anweisungen auf Vektoren mit einer beliebigen Anzahl von Komponenten anwenden.

2. 

   
   
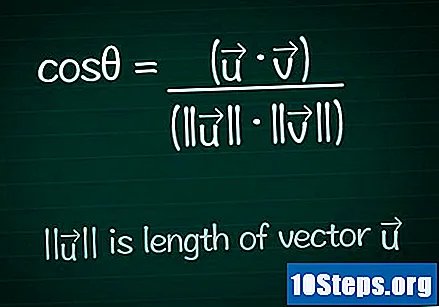
   Schreiben Sie die Kosinusformel. Um den Wert des Winkels θ zwischen zwei beliebigen Vektoren zu ermitteln, müssen wir zuerst den Kosinus dieses Winkels berechnen. Sie können die Formel im Detail suchen und herausfinden oder sie einfach wie folgt schreiben:
   • cosθ = (•) / (|||| ||||)
   • |||| repräsentiert die Modul (oder Länge) des Vektors ".
   • • repräsentiert die Skalarprodukt (oder internes Produkt) der beiden Vektoren.

3. 

   
   
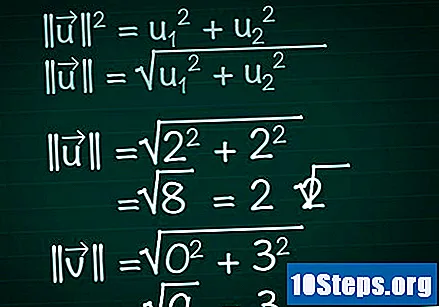
   Berechnen Sie den Modul jedes Vektors. Stellen Sie sich ein rechtwinkliges Dreieck vor, das von der Komponente gebildet wird x eines Vektors, seiner Komponente y und der Vektor selbst. In diesem Dreieck spielt der Vektor die Rolle der Hypotenuse; Um seine Länge zu finden, wenden wir daher den Satz von Pythagoras an. Infolgedessen ist diese Formel leicht auf Vektoren mit einer beliebigen Anzahl von Komponenten anwendbar.
   • || u || = u₁ + u₂. Wenn der Vektor mehr als zwei Komponenten hat, fügen Sie einfach + u hinzu₃ + u₄ +...
   • Daher müssen wir für einen zweidimensionalen Vektor || u || = √ (u₁ + u₂).
   • In unserem Beispiel |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Berechnen Sie das Skalarprodukt zwischen den beiden Vektoren. Sie sollten bereits die Methode zum Multiplizieren von Vektoren kennen, die auch aufgerufen wird Skalarprodukt. Um das Skalarprodukt zweier Vektoren in Bezug auf ihre Komponenten zu berechnen, multiplizieren wir die Komponenten in derselben Richtung miteinander und addieren dann die Ergebnisse dieser Produkte.
   • Wenn Sie mit Computergrafikprogrammen arbeiten, besuchen Sie zuerst den Abschnitt "Tipps", bevor Sie fortfahren.
   • In mathematischen Begriffen, • = u₁v₁ + u₂v₂, wobei u = (u₁u₂). Wenn Ihr Vektor mehr als zwei Komponenten enthält, fügen Sie einfach + u hinzu₃v₃ + u₄v₄...
   • In unserem Beispiel ist • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dies ist der Wert des Skalarprodukts zwischen den Vektoren und.

5. 

   Ersetzen Sie diese Ergebnisse durch die Kosinusformel. Denken Sie daran, cosθ = (•) / (|||| || ||). Wir haben bereits das Skalarprodukt und das Modul der beiden Vektoren berechnet. Ersetzen wir nun diese Werte in der Formel und berechnen den Kosinus des Winkels.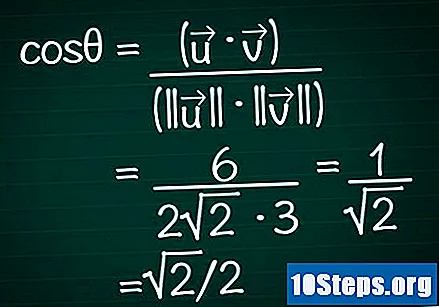
   • In unserem Beispiel ist cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Finden Sie den Winkel basierend auf Ihrem Kosinus.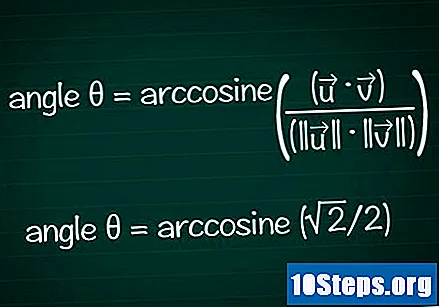
   Verwenden Sie die Bogen- oder Cos-Funktion Ihres Rechners, um den Winkel θ aus Ihrem Cosinuswert zu bestimmen. In einigen Fällen können Sie den Winkelwert möglicherweise anhand des Einheitskreises ermitteln.
   • In unserem Beispiel ist cosθ = √2 / 2. Geben Sie "arccos (√2 ​​/ 2)" in Ihren Rechner ein, um den Winkel zu ermitteln. Eine andere Möglichkeit besteht darin, nach dem Winkel θ des Einheitskreises zu suchen, wobei cosθ = √2 / 2 ist. Dies gilt für θ = /₄ oder 45 °.
   • Wenn wir alle Informationen zusammenfassen, erhalten wir die endgültige Formel θ = Arccosin ((•) / (|||| || ||))

Teil 2 von 2: Definieren der Formel zur Berechnung des Winkels

1. 

   Verstehe den Zweck der Formel. Die Formel, mit der wir den Winkel zwischen zwei Vektoren berechnet haben, wurde nicht aus bereits vorhandenen Regeln abgeleitet. Stattdessen wurde es als Definition des Skalarprodukts zwischen zwei Vektoren und des Winkels zwischen ihnen erstellt. Diese Entscheidung ist jedoch nicht willkürlich. Bei näherer Betrachtung der Grundgeometrie können wir sehen, warum diese Formel zu so nützlichen und intuitiven Definitionen führt.
   • In den folgenden Beispielen werden zweidimensionale Vektoren verwendet, da sie der intuitivste Typ sind, mit dem gearbeitet werden kann. Bei Vektoren mit drei oder mehr Dimensionen werden die Eigenschaften aus der allgemeinen Formel definiert (ebenfalls auf sehr ähnliche Weise).

2. 

   Überprüfen Sie das Kosinusgesetz. Betrachten Sie in jedem Dreieck den Winkel θ, der von den Seiten gebildet wird Das und B. und die Seite ç gegenüber diesem Winkel. Nach dem Kosinusgesetz ist c = a + b -2abBund(θ). Die Demonstration dieser Formel kann leicht aus der Kenntnis der Grundgeometrie erhalten werden.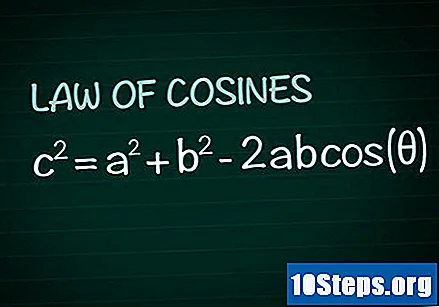

3. 

   Verbinden Sie die beiden Vektoren zu einem Dreieck. Zeichnen Sie ein Paar Vektoren und mit einem Winkel θ zwischen ihnen. Zeichnen Sie dann einen dritten Vektor zwischen sich, um ein Dreieck zu bilden. Mit anderen Worten, zeichnen Sie den Vektor so, dass + = oder einfach = -.

4. 

   Wenden Sie das Kosinusgesetz auf dieses Dreieck an. Ersetzen Sie die Länge der Seiten unserer Vektordreieck (dh das Vektormodul) in der Formel für das Kosinusgesetz:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||Bund(θ)

5. 

   Schreiben Sie die Formel mit skalaren Produkten neu. Denken Sie daran, dass das Punktprodukt die Vergrößerung eines auf einen anderen projizierten Vektors ist. Das Skalarprodukt eines Vektors selbst erfordert keine Projektion, da sich die Richtung nicht ändert. Dies bedeutet, dass • = || a ||. Schreiben wir anhand dieser Informationen die Gleichung des Kosinusgesetzes neu:
   • (-) • (-) = • + • - 2 || a || || b ||Bund(θ)

6. 

   Vereinfachen Sie die Formel. Erweitern Sie die Produkte auf der linken Seite der Gleichung und vereinfachen Sie sie, bis Sie die Formel erreichen, die wir zur Berechnung von Winkeln kennen.
   • • - • - • + • = • + • - 2 || a || || b ||Bund(θ)
   • - • - • = -2 || a || || b ||Bund(θ)
   • -2 (•) = -2 || a || || b ||Bund(θ)
   • • = || a || || b ||Bund(θ)

Tipps

• Wenden Sie zur schnellen Auflösung die folgende Formel auf jedes zweidimensionale Vektorpaar an: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Wenn Sie mit Computergrafikprogrammen arbeiten, müssen Sie höchstwahrscheinlich nur die Richtung der Vektoren kennen, nicht deren Länge. Führen Sie die folgenden Schritte aus, um die Gleichungen zu vereinfachen und Ihr Programm zu beschleunigen:
  • Normalisieren Sie jeden Vektor, dh suchen Sie den Einheitsvektor, der dieselbe Richtung wie der ursprüngliche Vektor hat. Teilen Sie dazu jede Komponente des Vektors durch das Vektormodul.
  • Berechnen Sie das Skalarprodukt der normalisierten Vektoren, nicht der ursprünglichen Vektoren.
  • Da der Modul (dh die Länge) der normalisierten Vektoren einheitlich ist, können wir sie aus der Formel herauslassen. Ihre endgültige Gleichung für die Berechnung von Winkeln lautet Bögen (•).
• Anhand der Formel des Kosinusgesetzes können wir schnell herausfinden, ob der betreffende Winkel spitz oder stumpf ist. Beginnen Sie mit cosθ = (•) / (|||| ||||):
  • Die linke und rechte Seite der Gleichung müssen das gleiche Vorzeichen haben (positiv oder negativ).
  • Da die Längen immer positiv sind, hat cosθ immer das gleiche Vorzeichen wie das Skalarprodukt.
  • Wenn daher das Skalarprodukt positiv ist, ist cos & thgr; positiv. Dies bedeutet, dass der Winkel im ersten Quadranten des Einheitskreises liegt, dh θ <π / 2 oder 90 °. Daher ist der Winkel spitz.
  • Wenn das Skalarprodukt negativ ist, ist cosθ negativ. Dies bedeutet, dass der Winkel im zweiten Quadranten des Einheitskreises liegt, dh π / 2 <θ ≤ π oder 90 ° <θ ≤ 180 °. Daher ist der Winkel stumpf.